Decomposition Tutorial

Creating Sweepable Volumes Through Webcutting

Most volumes require some measure of decomposition before they can be meshed with a hexahedral meshing scheme. The most common hexahedral meshing tool is the sweeping algorithm. Sweeping is the process of creating a hexahedral mesh by extruding a quadrilateral surface mesh from a source surface onto a topologically similar target surface by way of a linking surface. The surface mesh can be meshed with any surface meshing scheme (i.e. structured or unstructured mesh), but the most common surface meshing scheme for the sweeping algorithm is the pave scheme. In fact, the sweeping algorithm is sometimes called the "pave-sweep" algorithm. Most volumes aren't automatically sweepable, which is why geometry decomposition is so important to the meshing process. Decomposition usually involves a series of webcutting, Boolean, and virtual geometry operations that break up a larger model into sweepable regions. Studies have shown that this step in the meshing process is the most time consuming for the analyst. The goals of this tutorial are for the user to learn to:

1. Recognize sweepable volumes
2. Recognize how to decompose a model into sweepable parts
3. Gain proficiency with webcutting and other decomposition techniques
4. Avoid common pitfalls with decomposition and sweeping

Why use sweeping?

Of all the hexahedral meshing schemes in the Coreform Cubit toolkit, sweeping is considered the most reliable at producing high quality elements. Although decomposing a model into sweepable volumes can be time-consuming, and sometimes falls into the realm of trying to fit a square peg into a round hole, the pave-sweep algorithm has a high rate of success, and it sometimes the only way to get a hexahedral mesh on a model.

What makes a volume sweepable?

Recognizing sweepable topologies can be an art form. Sweepable volumes can be comprised of many different topologies. We typically classify sweeping problems into three groups, based on the number of source/target surfaces.

Basic Sweep Groups

One-to-one: A volume with a one source surface and one target surface.

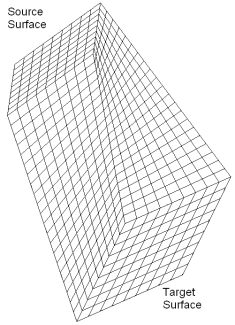
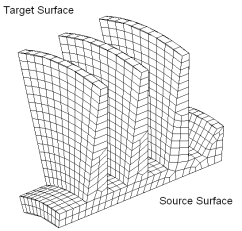
Many-to-one: A volume with multiple source surfaces and one target surface

Multisweep (or Many-to-Many): A volume with multiple target surfaces

Points to consider when determining whether a volume is sweepable

• Swept surface meshes can be extruded through a volume which is rotated or translated. However, if the translation/rotation is severe then the quality of the resulting mesh may be poor.
• A volume with multiple target surfaces and a single source surface can sometimes be inverted and handled as a many-to-one sweepable volume. Otherwise, it is treated as a multisweep problem.
• Imprinting introduces new topology onto surfaces. Sweepable volumes may not be sweepable after imprinting and merging adjacent surfaces
• Multisweep is still under development, and has limitations, so if you are having difficulty with the multisweep algorithm, it is usually a good idea to decompose it into many-to-one or one-to-one sweepable regions.
• Coreform Cubit won’t always automatically recognize your volume as a sweepable volume, even if it is. Sometimes, you have to give it a list of source/target surfaces explicitly.

Basic Sweep Paths

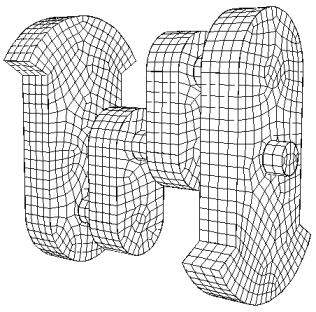
In addition to the different topologies, sweepable volumes can be classified by the sweep direction. These include: top-to-bottom, inside-to-outside, and around (rotational). Be sure to consider all the possibilities for sweep directions when you begin decomposing a model. And keep in mind that sweep paths must be compatible with adjacent volumes. To be compatible, overlapping surfaces must have the same scheme (i.e. both must be a linking surface or a paved surface). The volume below is meshed three different times with the three different sweep directions. Notice the difference in element sizes and orientations between the meshes. See if you can pick out the different source and target surfaces in each example. As an exercise, try to mesh this model with each of the different sweep paths.

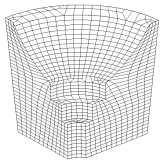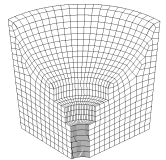Top-to-Bottom	Inside-to-Outside	Around (Rotational)
Many-to-one	Many-to-one	One-to-one (this is the default sweep direction for this model)

What are some good strategies for decomposing my model?

Recognizing when a volume is sweepable is a difficult task of itself, but being able to come up with viable webcutting, compositing, and Boolean strategies to make a volume sweepable is even more difficult, and can only be achieved through practice. Here are some general principles to follow when decomposing a model:

1. Select your sweep path
2. Use as few webcuts as possible
3. Set your own source and target surfaces if Coreform Cubit does not pick them automatically
4. If one of your volumes does not mesh, or has an undesirable mesh, try changing the order in which you mesh volumes. This will hardset the intervals on the volumes.
5. The Reset Volume command will remove all schemes and interval settings from volumes.
6. If changing the mesh order or resetting the volumes does not work and you continue to get "Matching Intervals Failed" errors, set explicit intervals on some or all curves.
7. Make additional webcuts if necessary.
8. Check for sliver surfaces or curves that may have been introduced during decomposition and remove these through tweaking collapsing, or compositing.
9. Change surface vertex types on mapped or submapped surfaces if you need to force a certain configuration
10. Use partitioning to introduce virtual geometry constraints without affecting the underlying geometry
11. Composite surfaces to remove constraints without affecting the underlying geometry
12. Save your work often. For a complex model, the meshing process can be very iterative. You may need to start over many times until you find an acceptable solution.

The following is a compilation of several different decomposition problems of varying difficulty. If you accessed this help from the Coreform Cubit program (as opposed to the web documentation), you will need to browse for the geometry files from within your Coreform Cubit installation directory. They should be located in the "/components/Coreform Cubit/help/step_by_step_tutorials/decomposition" directory of the Coreform Cubit installation folder.

Example	Image	File
Beginner
Sweeping through multiple adjacent volumes		example01.sat
Interlocking rings		example02.sat
Webcutting using the "sweep" option		example03.sat
Using the loft command		example04.sat
Multiple sweep directions		example05.sat
Advanced
Employing symmetry and controlling skew		example06.sat
Using virtual geometry		example07.sat
Sweeping volumes with narrow angles and surfaces		example08.sat