Example 7. Using virtual geometry in geometry decomposition

Virtual geometry is used to change the properties of mesh without changing the underlying geometry. The next example uses virtual geometry to remove unwanted sliver curves, and to create a sweepable volume. The composite curve function is used to combine sliver curves that are created from webcutting a slightly curved surface. Then the partition surface command is used to create additional partitions on a surface to ensure sweepability.

Suggested webcuts

Webcut	Command
	Coreform Cubit> webcut volume 1 sweep surface 2 vector 0 0 -1 through_all
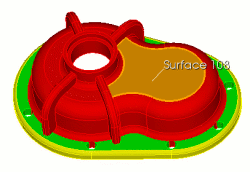	Coreform Cubit> webcut volume 3 sweep surface 108 vector 0 0 -1 through_all
	Coreform Cubit> webcut volume 3 sweep surface 13 vector 0 0 -1 through_all Coreform Cubit> webcut volume 3 sweep surface 28 vector 0 0 -1 through_all Coreform Cubit> webcut volume 3 sweep surface 74 vector 0 0 -1 through_all
	Coreform Cubit> webcut volume 3 with sheet extended from surface 197
	Coreform Cubit> webcut volume 8 with sheet extended from surface 224
	Coreform Cubit> webcut volume 11 10 12 9 with plane surface 28
	Coreform Cubit> webcut volume 3 with plane normal to curve 116 fraction 0.5
	Coreform Cubit> webcut volume 3 17 with plane normal to curve 835 close_to vertex 487
	Coreform Cubit> webcut volume 18 19 with sheet extended from surface 376
	Coreform Cubit> webcut volume 3 17 with sheet extended from surface 378
	Coreform Cubit> webcut volume 8 with sheet extended from surface 73 Coreform Cubit> webcut volume 8 with sheet extended from surface 72 Coreform Cubit> webcut volume 8 with sheet extended from surface 133 Coreform Cubit> webcut volume 8 with sheet extended from surface 71
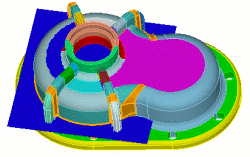	Coreform Cubit> webcut volume 8 with plane vertex 709 vertex 713 vertex 702
	Coreform Cubit> unite volume 36 45 Coreform Cubit> unite volume 37 43 Coreform Cubit> unite volume 35 44 Coreform Cubit> unite volume 39 42
	Coreform Cubit> webcut volume 29 with plane vertex 81 vertex 93 vertex 154
	Coreform Cubit> unite volume 33 36 50 11 Coreform Cubit> unite volume 10 49 37 31 Coreform Cubit> unite volume 12 52 35 34 Coreform Cubit> unite volume 9 51 39 32 Coreform Cubit> unite volume 9 22 Coreform Cubit> unite volume 12 23 Coreform Cubit> unite volume 20 33 Coreform Cubit> unite volume 21 10
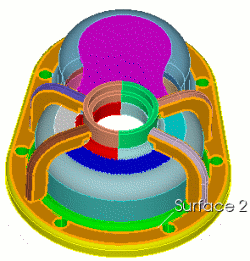
	Coreform Cubit> webcut volume 12 with plane vertex 86 vertex 71 vertex 76 Coreform Cubit> webcut volume 53 with plane vertex 738 vertex 87 vertex 741 Coreform Cubit> webcut volume 12 with plane vertex 72 vertex 85 vertex 74 Coreform Cubit> webcut volume 55 with plane vertex 754 vertex 205 vertex 208 Coreform Cubit> webcut volume 12 sweep surface 731 along curve 1073 through_all Coreform Cubit> unite volume 53 57 56 Coreform Cubit> unite volume 54 12 55 Coreform Cubit> webcut volume 9 with plane vertex 99 vertex 101 vertex 103 Coreform Cubit> webcut volume 58 with plane vertex 769 vertex 98 vertex 772 Coreform Cubit> webcut volume 9 with plane vertex 106 vertex 104 vertex 100 Coreform Cubit> webcut volume 60 with plane vertex 781 vertex 201 vertex 198 Coreform Cubit> webcut volume 9 sweep surface 764 along curve 1078 through_all Coreform Cubit> unite volume 58 62 60 Coreform Cubit> unite volume 59 9 61 Coreform Cubit> webcut volume 20 with plane vertex 140 vertex 138 vertex 135 Coreform Cubit> webcut volume 63 with plane vertex 139 vertex 137 vertex 134 Coreform Cubit> webcut volume 20 with plane vertex 141 vertex 800 vertex 796 Coreform Cubit> webcut volume 64 with plane vertex 803 vertex 220 vertex 223 Coreform Cubit> webcut volume 63 sweep surface 803 along curve 1238 through_all Coreform Cubit> unite volume 20 67 66 Coreform Cubit> unite volume 65 63 64 Coreform Cubit> webcut volume 21 with plane vertex 165 vertex 163 vertex 160 Coreform Cubit> webcut volume 68 with plane vertex 164 vertex 162 vertex 159 Coreform Cubit> webcut volume 21 with plane vertex 825 vertex 169 vertex 822 Coreform Cubit> webcut volume 69 with plane vertex 830 vertex 216 vertex 213 Coreform Cubit> webcut volume 68 sweep surface 836 along curve 1069 through_all Coreform Cubit> unite volume 21 72 69 Coreform Cubit> unite volume 70 68 71 These are the steps to webcut each of the stiffeners into the configuration shown. It is repeated for each of the stiffeners. This is also the step which creates the sliver curves which must be composited out later.
	Coreform Cubit> webcut volume 70 65 59 54 with plane surface 2
	Coreform Cubit> unite volume 1 76 75 73 74
	Coreform Cubit> unite volume 28 47 46 41 48 38 8 30 29 40
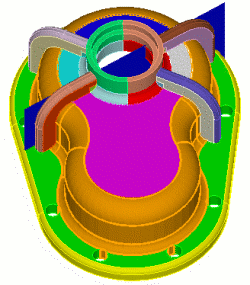	Coreform Cubit> webcut volume 28 with plane surface 870 Coreform Cubit> webcut volume 28 77 with plane surface 871 Coreform Cubit> webcut volume 28 77 with plane surface 878 Coreform Cubit> webcut volume 28 77 with plane surface 879
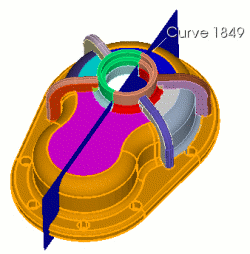	Coreform Cubit> webcut volume 1 81 2 82 with plane normal to curve 1849 fraction 0.5
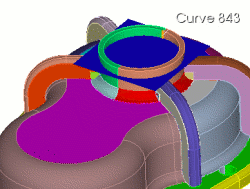	Coreform Cubit>webcut volume 19 18 with plane normal to curve 843 fraction 0.75
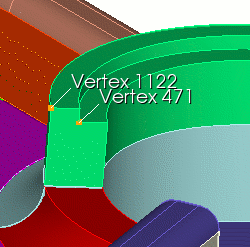	Coreform Cubit> create curve vertex 1122 vertex 471 on surface 1134
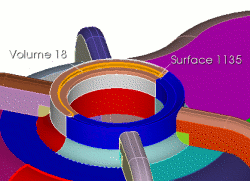	Coreform Cubit> webcut volume 19 sweep curve 2073 along curve 2042 through_all Coreform Cubit> webcut volume 18 with sheet extended from surface 1146 Coreform Cubit> webcut volume 18 with sheet extended from surface 1135
	Coreform Cubit> unite volume 91 92 Coreform Cubit> delete curve 2073
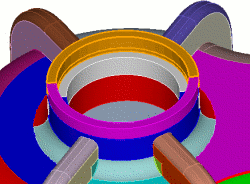	Coreform Cubit> unite volume 89 18 Coreform Cubit> unite volume 88 19 Coreform Cubit> imprint all Coreform Cubit> merge all
	Composite small curves formed from webcuts Coreform Cubit> composite create curve 1456 1468 Coreform Cubit> composite create curve 1459 1467 Coreform Cubit> composite create curve 1499 1511 Coreform Cubit> composite create curve 1502 1510 Coreform Cubit> composite create curve 1371 1379 Coreform Cubit> composite create curve 1370 1381 Coreform Cubit> composite create curve 1423 1413 Coreform Cubit> composite create curve 1422 1414 Coreform Cubit> volume all scheme auto
	Create the partitioned curves shown using existing vertices Coreform Cubit> partition create surface 1067 vertex 311 175 Coreform Cubit> partition create surface 1067 vertex 174 312 Coreform Cubit> partition create surface 1063 vertex 123 294 Coreform Cubit> partition create surface 1251 vertex 170 226 Coreform Cubit> partition create surface 1082 vertex 195 115 Coreform Cubit> partition create surface 1082 vertex 242 116 Coreform Cubit> partition create surface 1077 vertex 117 309 Coreform Cubit> partition create surface 1255 vertex 118 310
	Meshing order is significant in this case. Since meshing a volume will hard set the interval counts on curves and surfaces, you will need to make sure that all of the interval counts are the same on adjacent volumes. Usually the meshing algorithm can handle this interval matching, but sometimes it helps to mesh volumes in a certain order. In this case, the meshing order also significantly changes the quality in the resulting mesh. 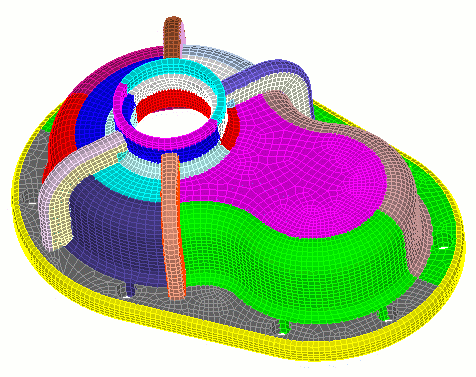Coreform Cubit> reset volume all Coreform Cubit> volume all scheme auto Coreform Cubit> volume 81 scheme sweep source surface 979 target surface 1061 rotate off Coreform Cubit> volume 81 sweep smooth auto Coreform Cubit> volume 85 scheme sweep source surface 1061 target surface 889 rotate off Coreform Cubit> volume 85 sweep smooth auto Coreform Cubit> volume all size 0.1 Coreform Cubit> curve 2125 2122 interval 12 Coreform Cubit> mesh vol 5 6 7 13 14 15 16 (COLORED GREEN) Coreform Cubit> mesh Volume 85 81 77 83 78 82 87 28 80 79 (COLORED RED) Coreform Cubit> mesh vol 88 89 91 90 17 3 (COLORED YELLOW) Coreform Cubit> mesh volume with not is_meshed (COLORED WHITE)

Final mesh

The final mesh is shown below.