Coreform Cubit tutorial: Python scripting to enable spline construction over complex geometries

Background

A biomedical stent device has been modeled and meshed with beam elements for initial analysis. More substantive subsequent analysis, however, requires a full 3D representation of the device. Ordinarily, a 3D representation might be obtained by sweeping a surface along the model’s beam elements.

However, this option is not readily available because when imported into Cubit as a NASTRAN file, the model is recognized as a faceted part rather than a sweepable object. The next logical step is to try to fit a spline through the beam elements in order to create an ACIS object that itself can be swept. But to accomplish this, Cubit must be supplied with the model’s element ordering / connectivity information.

In this tutorial, we demonstrate how to use Python scripting to extract and provide this connectivity information and thus enable spline construction over the beam-element stent model.

Overview

First, recognize that a mesh consists of two main data structures:

Element connectivity (topology)
Nodal coordinates (geometry)

Element connectivity arrays can be represented as a graph which then allows us to make use of various graph theory algorithms. For example, since the node numbers are unordered (the node ids do not increase monotonically from one end to the other), we will compute the ordered arrangement of nodes associated with each wire via the following steps:

Convert element connectivity array into an undirected graph
Extract subgraphs representing each wire by computing the connected components of the graph.
Find the boundary nodes of each wire’s graph
Compute the simple directed path between the two boundary nodes of each wire’s graph

Then, once we have the path for each wire, we can build a spline through the nodes and sweep a circle along the path.

Main routine

Our main method sets some important Cubit settings to improve performance, before creating the geometry and meshing. Note that on my laptop I can create all the geometry and export the geometry within a couple minutes, but meshing takes approximately 2-3 hours.

def main():
  # Some default settings for improved performance
  cubit.cmd( "echo off" )
  cubit.cmd( "undo off" )
  cubit.cmd( "warning off" )
  cubit.cmd( "set Default Autosize off" )  # CRITICAL
  # Build the stent geometry and mesh
  cubit.cmd( "reset" )
  load_mesh( filename )
  wire_graphs = generate_wire_graphs()
  generate_wires_from_graph( wire_graphs )
  save_cad()
  mesh_all_wires()
  save_mesh()

Setup script execution

Many Python scripts use the if __name__ == "__main__": statement. Here’s how implement it to allow me to run the script either from the Cubit GUI or from an external Python environment.

if __name__ == "__main__":
  import sys
  sys.path.append( r"C:\Program Files\Coreform Cubit 2023.11\bin" )
  import cubit
  main()
elif __name__ == "__coreformcubit__":
  main()

Generate wire graphs

Importing the mesh is straightforward. Note the usage of Python’s f-string functionality, which we will use liberally in this script.

def load_mesh( filename ):
  cubit.cmd( f"import nastran '{filename}'" )

Once we’ve loaded the mesh we can query the mesh connectivity and create the undirected graphs for each wire. In the below routine notice that we initialize an undirected graph for the entire model’s mesh using networkx.Graph(). We can then fill our graph by adding each element as an edge. Then we use networkx.connected_componnents() to get an undirected graph for each wire.

def generate_wire_graphs():
  E = cubit.get_entities( "edge" )
  N = cubit.get_entities( "node" )
  CONN = numpy.zeros( (2,len(E)), dtype="int" )
  CONN_graph = networkx.Graph()
  for e in range( 0, len(E) ):
    eid = E[e]
    CONN[:,e] = cubit.get_connectivity( "edge", eid )
    CONN_graph.add_edge( CONN[0,e], CONN[1,e] )
  components = [ c for c in networkx.connected_components(CONN_graph) ]
  subgraphs = [ CONN_graph.subgraph(c).copy() for c in components ]
  return subgraphs

Generate wires from graphs

This first routine may appear a bit superfluous: it simply loops through each subgraph and generates a wire. The routine is important, however, for performance reasons. Note that each wire includes approximately 1000 vertices. If every vertex-generation command is rendered and produces terminal output, wire creation can become computationally burdensome. This routine allows us to toggle off the graphics and information output for more efficient wire creation.

Note that when running Python from within Coreform Cubit, the print() command will not print to the terminal.

Performance considerations also make it prudent to change a standard Cubit setting that can cause significant performance issues when working with complex geometries. Whenever a geometric entity is created, Cubit ordinarily computes a default mesh size. For geometries like these wires, this computation can take several minutes. Accordingly, we’ll turn off this behavior at the beginning of the script with set Default Autosize off. (Note that doing so means that we must be sure to explicitly define mesh sizing later.)

def generate_wires_from_graph( subgraphs ):
    for c in range( 0, len( graph ) ):
        print( f"GENERATING WIRE {c+1} OF {len( subgraphs )}" )
        cubit.cmd( "graphics off" )
        cubit.cmd( "info off" )
        generate_wire_from_graph_component( subgraphs[c] )
        cubit.cmd( "graphics on" )
        cubit.cmd( "info on" )
        print( "#"*20 )

Generate wires from graph components

This next method is a big one. You’ll notice also that it depends on the prior definition of a custom method called find_path_order(), which finds a node at one end of the wire, then finds the node ordering to reach the other end.

Side note: The networkx package may offer a better way to accomplish this purpose (computing a path graph); however, as of this writing we have been unable to find a simpler approach that worked.

def find_path_order( graph ):
    # Find nodes with valence 1
    endpoints = [node for node in graph.nodes() if graph.degree(node) == 1]
    # Choose one of the endpoints as the starting point for DFS
    start_node = endpoints[0]
    # Perform a depth-first search and get the nodes in order
    ordered_nodes = list( networkx.dfs_preorder_nodes( graph, source=start_node ) )
    return ordered_nodes

We then create a circular surface, rotate it so that its face-normal aligns to the tangent of the spline at its starting vertex, move it to the starting vertex, and then sweep it along the spline curve to create the wire’s volume. (While we here use the cubit.Dir() object, we could have instead used the numpy package’s linear algebra routines.)

Next, because we expect it will help with meshing, we split the periodic surface of the resulting wire.

def generate_wire_from_graph_component( component ):
    ordered_nodes = find_path_order( component )
    ordered_verts = []
    for nid in ordered_nodes:
        x, y, z = cubit.get_nodal_coordinates( int( nid ) )
        cubit.cmd( f"create vertex {x} {y} {z}" )
        ordered_verts.append( cubit.get_last_id( "vertex" ) )
    cubit.cmd( f"create curve spline location vertex {cubit.get_id_string( ordered_verts )} delete" )
    curve_id = cubit.get_last_id( "curve" )
    curve = cubit.curve( curve_id )
    start_vert_id, stop_vert_id = cubit.parse_cubit_list( "vertex", f"in curve {curve_id}" )
    start_vert = cubit.vertex( start_vert_id )
    cubit.cmd( f"create surface circle radius {radius} zplane" )
    sid = cubit.get_last_id( "surface" )
    face_normal = cubit.Dir( 0, 0, 1 )
    tx, ty, tz = curve.tangent( start_vert.coordinates() )
    orientation = cubit.Dir( tx, ty, tz )
    rot_axis = orientation.cross( face_normal ).get_xyz()
    rot_angle = numpy.rad2deg( orientation.dot( face_normal ) ) + 90
    cubit.cmd( f"rotate Surface {sid} angle {rot_angle} about origin 0 0 0 direction {rot_axis[0]} {rot_axis[1]} {rot_axis[2]}" )
    cubit.cmd( f"move Surface {sid} location vertex {start_vert_id} include_merged" )
    cubit.cmd( f"sweep surface {sid} along curve {curve_id}  keep  individual" )
    vid = cubit.get_last_id( "volume" )
    cubit.cmd( f"split periodic vol {vid}" )
    cubit.cmd( "delete surface all" )
    cubit.cmd( "delete curve all" )
    cubit.cmd( "delete vertex all" )
    cubit.cmd( "compress ids" )

Mesh the wires

Meshing the wires uses the same two-method approach used to create the mesh geometry — again to allow for some modifications to settings and printing output.

def mesh_all_wires():
    V = cubit.get_entities( "volume" )
    for v in range( 0, len( V ) ):
        print( f"MESHING WIRE {v+1} OF {len( V )}" )
        cubit.cmd( "graphics off" )
        cubit.cmd( "info off" )
        vid = V[v]
        mesh_wire( vid )
        cubit.cmd( "graphics on" )
        cubit.cmd( "info on" )
        print( "#"*20 )

For mesh quality I want to manually specify the sweep meshing scheme for each wire, including specifying a circle mesh scheme on the source surface. The original mesh has some highly skewed elements:

which will improve significantly with the jacobian volume smooth scheme:

Both the meshing and smooth algorithms are relatively slow due to the expense of evaluating such a large and complicated spline surface. This consideration motivates the separation of the geometry creation routines from meshing routines. It is also the reason we set a fairly loose tolerance, of 0.1, for the smoothing operation.

def mesh_wire( wire_vol_id ):
    vol_surf_ids = cubit.parse_cubit_list( "surface", f"in volume {wire_vol_id}" )
    source_surf_id = None
    target_surf_id = None
    link_surf_ids = []
    for sid in vol_surf_ids:
        if cubit.get_surface_type( sid ) == "plane surface":
            if source_surf_id is None:
                source_surf_id = sid
            else:
                target_surf_id = sid
        else:
            link_surf_ids.append( sid )
    cubit.cmd( f"volume {wire_vol_id} redistribute nodes on" )
    cubit.cmd( f"volume {wire_vol_id} scheme Sweep  source surface {source_surf_id} target surface {target_surf_id} sweep transform translate propagate bias" )
    cubit.cmd( f"volume {wire_vol_id} autosmooth target off" )
    cubit.cmd( f"volume {wire_vol_id} size {radius}" )
    cubit.cmd( f"surface {source_surf_id} scheme circle" )
    cubit.cmd( f"surface {source_surf_id} size {0.7*radius}" )
    cubit.cmd( f"mesh volume {wire_vol_id}" )
    cubit.cmd( f"set smooth tolerance {0.1}" )
    cubit.cmd( f"volume {wire_vol_id} smooth scheme laplacian free" )
    cubit.cmd( f"smooth volume {wire_vol_id}" )

Results

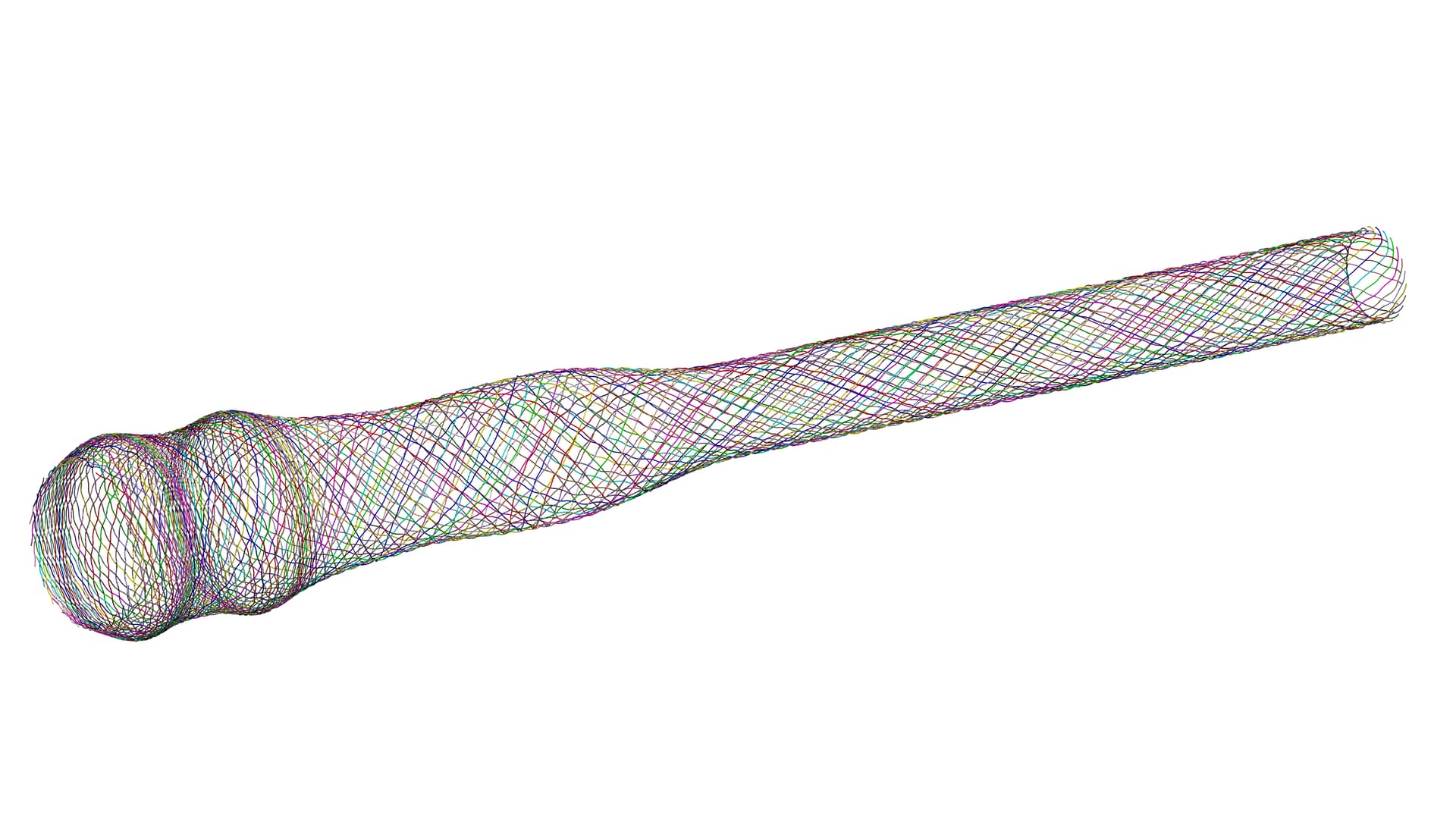
The resulting 3D representation is pictured below, first in its entirety and then with a closeup view. Hopefully this helps demonstrate the use of Cubit’s Python API, and of the wider Python ecosystem, as a pretty powerful tool!