Coreform Cubit Python API: Object-Based API
The object-based API provides a more “pythonic” interface. This interface is maintained and tested. There are object modification methods that are not documented here. Those methods are deprecated and are not under current development.
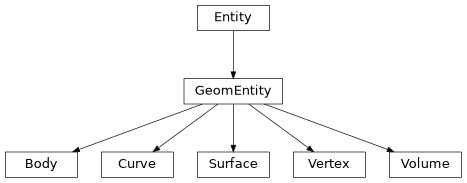
The leaf objects correspond to entities in Coreform Cubit.
They are derived from GeomEntity and
Entity. All
methods defined in
the base classes are available in the leaf classes.
Cubit entities should be created
using the cmd method.
There are operators to convert from an id to an object and
back. For example,
Objects can be useful to track and store ids and state.
Object Creation Methods
Cubit objects are created from an id and return an object of the given type.
- cubit.body(id_in)
-
Creates a body object from an ID
- Parameters:
-
id_in (int) – The ID of the body
- Returns:
-
The body object
- Return type:
- cubit.volume(id_in)
-
Creates a volume object from an ID
- Parameters:
-
id_in (int) – The ID of the volume
- Returns:
-
The volume object
- Return type:
- cubit.surface(id_in)
-
Creates a surface object from an ID
- Parameters:
-
id_in (int) – The ID of the surface
- Returns:
-
The surface object
- Return type:
- cubit.curve(id_in)
-
Creates a curve object from an ID
- Parameters:
-
id_in (int) – The ID of the curve
- Returns:
-
The curve object
- Return type:
- cubit.vertex(id_in)
-
Creates a vertex object from an ID
- Parameters:
-
id_in (int) – The ID of the vertex
- Returns:
-
The vertex object
- Return type:
Entity
- class cubit.Entity
-
The base class of all the geometry and mesh types.
import cubit cubit.cmd('brick x 1 y 1 z 1') br = cubit.volume(1) bbox = br.bounding_box() cubit.cmd('delete body 1')- entity.bounding_box()
-
Get the bounding box of the Entity.
b_box = entity.bounding_box()- Returns:
-
The bounding box as a vector (or list) where the indices correspond to the values as follows:
-
0 - minimum x value
-
1 - minimum y value
-
2 - minimum z value
-
3 - maximum x value
-
4 - maximum y value
-
5 - maximum z value
- Return type:
-
tuple[float] length 6
- entity.center_point()
-
Get the center point of the Entity. Note that this is an approximate centroid.
center = entity.center_point()- Returns:
-
The center point as a list of length 3 where the indices correspond to the values as follows:
-
0 - x value
-
1 - y value
-
2 - z value
- Return type:
-
tuple[float], length 3
- entity.id()
-
Get the id of the Entity.
id = entity.id()- Returns:
-
The id of the Entity
- Return type:
-
int
- entity.is_visible()
-
Get the visibility state of the Entity.
vis = entity.is_visible()- Returns:
-
The current visiblity state of the Entity (1 if visible, 0 if not)
- Return type:
-
int
- entity.is_transparent()
-
Get the tranparency state of the Entity.
trans = entity.is_transparent()- Returns:
-
The current transparency state of the Entity (1 if transparent, 0 if not)
- Return type:
-
int
GeomEntity
- class cubit.GeomEntity(*args, **kwargs)
-
The base class for specifically the Geometry types (Body, Surface, etc.)
- GeomEntity.mesh()
-
Mesh the GeomEntity.
geomEntity.mesh()
- GeomEntity.is_meshed()
-
Return the current mesh state of the GeomEntity.
mesh = geomEntity.is_meshed()- Returns:
-
Whether the GeomEntity is meshed or not
- Return type:
-
boolean
- GeomEntity.smooth()
-
Smooths the mesh on the GeomEntity.
geomEntity.smooth()
- GeomEntity.remove_mesh()
-
Removes the mesh on the GeomEntity.
geomEntity.remove_mesh()
- GeomEntity.entity_name()
-
Return the first name of the GeomEntity.
name = geomEntity.entity_name()- Returns:
-
The first name of the GeomEntity
- Return type:
-
string
- GeomEntity.entity_names()
-
Return the all the names of the GeomEntity.
names = geomEntity.entity_names()- Returns:
-
A tuple strings containing all the names of the GeomEntity
- GeomEntity.dimension()
-
Get the dimensions of the GeomEntity.
dim = geomEntity.dimension()- Returns:
-
The dimension of the GeomEntity
- Return type:
-
int
- GeomEntity.bodies()
-
Get the bodies in the GeomEntity.
bodies = geomEntity.bodies()- Returns:
-
A tuple of bodies contained within the GeomEntity
- GeomEntity.volumes()
-
Get the volumes in the GeomEntity.
volumes = geomEntity.volumes()- Returns:
-
A tuple of volumes contained within the GeomEntity
- GeomEntity.surfaces()
-
Get the surfaces in the GeomEntity.
surfaces = geomEntity.surfaces()- Returns:
-
A tuple of surfaces contained within the GeomEntity
- GeomEntity.curves()
-
Get the curves in the GeomEntity.
curves = geomEntity.curves()- Returns:
-
A tuple of curves contained within the GeomEntity
- GeomEntity.vertices()
-
Get the vertices in the GeomEntity.
vertices = geomEntity.vertices()- Returns:
-
A tuple of vertices contained within the GeomEntity
Body
The Body class contains a Cubit body and provides methods to query the body.
- class cubit.Body(*args, **kwargs)
-
Defines a body object that mostly parallels Cubit’s Body class
- body.get_mass_props()
-
Get the mass properties of the Body, specifically the center of gravity.
props = body.get_mass_props()- Returns:
-
A tuple of numerical data corresponding to the center of gravity of the body with indices as follows:
-
0 - x coordinate
-
1 - y coordinate
-
2 - z coordinate
- Return type:
-
tuple[float]
- body.point_containment(loc_in)
-
Get whether a point is in, on, or outside the Body.
on_out_in = body.point_containment([0,0,0])- Returns:
-
Whether a point is unknown (-1), outside (0), in (1), or on (2) the Body
- Return type:
-
int
- body.volume()
-
Get the volume of the Body.
vol = body.volume()- Returns:
-
The volume of the Body
- Return type:
-
float
- body.is_sheet_body()
-
Get whether the Body is a sheet body or not.
is_sheet = body.is_sheet_body()- Returns:
-
Whether the Body is a sheet body or not
- Return type:
-
boolean
Volume
The Volume class contains a Cubit volume and provides methods to query the volume.
- class cubit.Volume(*args, **kwargs)
-
Defines a volume object that mostly parallels Cubit’s RefVolume class
- volume()
-
Get the volume of the Volume.
vol = volume.volume()- Returns:
-
The volume of the Volume
- Return type:
-
float
- volume.color()
-
Get the color of the Volume.
col = volume.color()- Returns:
-
The color value associated with the volume’s current color. Note (0.,0.,0.,0.) denotes the default color with no assigned color value.
- volume.principal_axes()
-
Get the principal axes of the Volume.
axes = volume.principal_axes()- Returns:
-
A vector (or list) of the principal axes of the volume with the indices of the vector corresponding to the values as follows:
-
0 - axis 1 x value
-
1 - axis 1 y value
-
2 - axis 1 z value
-
3 - axis 2 x value
-
4 - axis 2 y value
-
5 - axis 2 z value
-
6 - axis 3 x value
-
7 - axis 3 y value
-
8 - axis 3 z value
- Return type:
-
tuple[float], length 9
- volume.principal_moments()
-
Get the principal moments of the Volume.
moments = volume.principal_moments()- Returns:
-
A vector (or list) of the principal moments of the volume with the indices of the vector corresponding to the values as follows:
-
0 - x moment
-
1 - y moment
-
2 - z moment
- Return type:
-
tuple[float], length 3
- volume.centroid()
-
Get the centroid of the Volume.
centroid = volume.centroid()- Returns:
-
A tuple of the coordinates of the centroid of the volume with the indices of the tuple corresponding to the values as follows:
-
0 - x coordinate
-
1 - y coordinate
-
2 - z coordinate
- Return type:
-
tuple[float], length 3
Surface
The Surface class contains a Cubit surface and provides methods to query the surface.
- class cubit.Surface(*args, **kwargs)
-
Defines a surface object that mostly parallels Cubit’s RefFace class
- surface.color()
-
Get the color of the surface.
col = surface.color()- Returns:
-
The color value associated with the volume’s current color. Note (0.,0.,0.,0.) denotes the default color with no assigne color value.
- Return type:
-
tuple[float], length 4 (r, g, b, a).
- surface.ordered_loops()
-
Get the ordered loops of the Surface where the first loop is the outer most loop.
loops = surface.ordered_loops()- Returns:
-
A tuple of tuples of Curves in loops
- Return type:
-
tuple[tuple[float]]
-
0, 0 - loop 1 curve 1
-
0, 1 - loop 1 curve 2
-
1, 0 - loop 2 curve 1
-
etc…
- surface.normal_at(location)
-
Get the normal at a particular point on the Surface.
norm = surface.normal_at([0,0,0])- Parameters:
-
location – A list or tuple containing three values that are the coordinates of a point
- Returns:
-
A tuple of floats representing values of normal vector as follows
- Return type:
-
tuple[float]
-
0 - x value
-
1 - y value
-
2 - z value
- surface.closest_point_trimmed(location)
-
Get the nearest point on the Surface to point specified.
nearest = surface.closest_point_trimmed([0,0,0])- Parameters:
-
location – A tuple containing three values that are the coordinates of a point
- Returns:
-
A vector (or list) of doubles representing values of nearest point as follows
- Return type:
-
tuple[float]
-
0 - x coordinate
-
1 - y coordinate
-
2 - z coordinate
- surface.closest_point_along_vector(location, along_vector)
-
Get the nearest point on the Surface to point specified along the specified vector.
nearest = surface.closest_point_along_vector([0,0,0], [1,1,1])- Parameters:
-
location – A list or tuple containing three values that are the coordinates of a point
- Returns:
-
A tuple of doubles representing values of nearest point as follows
- Return type:
-
tuple[float]
-
0 - x coordinate
-
1 - y coordinate
-
2 - z coordinate
- surface.point_containment(point_in)
-
Get whether a point is on or off of the Surface.
on_off = surface.point_containment([0,0,0])- Parameters:
-
point_in (tuple[float] length 3, in) – A vector containing three values that are the coordinates of a point
- Returns:
-
A python boolean representing whether the point is off (0) or on (1) the Surface
- Return type:
-
int
- surface.principal_curvatures(point)
-
Get the principal curvatures of the Surface.
curvatures = surface.principal_curvatures([0,0,0])- Parameters:
-
point (tuple[float], in) – A vector containing three values that are the coordinates of a point
- Returns:
-
A list of two floats representing the curvatures
- Return type:
-
tuple[float], length 2
-
0 - curvature 1
-
1 - curvature 2
- surface.position_from_u_v(u, v)
-
Get the Cartesian coordinates from the uv coordinates on the Surface.
pos = surface.position_from_u_v(0, 0)- Parameters:
-
-
u (float, in) – The u parameter
-
v – The v parameter
-
- Returns:
-
The Cartesian coordinates of the supplied uv coordinates as a vector.
- Return type:
-
tuple[float], length 3
-
0 - x coordinate
-
1 - y coordinate
-
2 - z coordinate
- surface.u_v_from_position(location)
-
Get the uv coordinates from the supplied Cartesian coordinates on the Surface.
uv = surface.position_from_u_v([0,0,0])- Parameters:
-
location (list[float] in) – A vector containing the Cartesian coordinates
- Returns:
-
The curvature values
- Return type:
-
tuple[float] length 2
-
0 - The u parameter
-
1 - The v parameter
- surface.get_param_range_U()
-
Get range of u for the Surface.
bounds = surface.get_param_range_U()- Returns:
-
The curvature values
- Return type:
-
tuple[float], length 2
-
0 - The lowest value in the u direction
-
1 - The highest value in the u direction
- surface.get_param_range_V()
-
Get range of v for the Surface.
lower_bound, upper_bound = surface.get_param_range_V()- Returns:
-
The curvature values
- Return type:
-
tuple[float], length 2
-
0 - The lowest value in the v direction
-
1 - The highest value in the v direction
- surface.area()
-
Get area of the Surface.
area = surface.area()- Returns:
-
The area of the Surface
- Return type:
-
float
- surface.is_planar()
-
Get whether the Surface is planar or not.
planar = surface.is_planar()- Returns:
-
Whether the Surface is planar or not
- Return type:
-
boolean
- surface.is_cylindrical()
-
Get whether the Surface is cylindrical or not.
cyl = surface.is_cylindrical()- Returns:
-
Whether the Surface is cylindrical or not
- Return type:
-
boolean
- surface.dihedral_angle(other, fraction)
-
Get the dihedral angle between this surface and another surface at a fraction along the shared curve between them.
- Parameters:
-
-
other (
Surface) – The other surface object used to form the dihedral angle -
fraction (float) – The fraction along the shared curve at which to calculate the dihedral angle (0.0 – 1.0)
-
- Returns:
-
the dihedral angle between the surfaces, in radians
- Return type:
-
float
Curve
The Curve class contains a Cubit curve and provides methods to query the curve.
- class cubit.Curve(*args, **kwargs)
-
Defines a curve object that mostly parallels Cubit’s RefEdge class
- curve.color()
-
Get the color of the Curve.
col = curve.color()- Returns:
-
The color value associated with the volume’s current color. Note (0.,0.,0.,0.) denotes the default color with no assigne color value.
- curve.tangent(point)
-
Get the tangent to the Curve at a particular point.
tan = curve.tangent([0,0,0])- Parameters:
-
point (tuple[float], length 3 , in) – A vector containing 3 doubles representing coordinates of a location on the Curve
- Returns:
-
The tangent to the Curve at the location specified
- Return type:
-
tuple[float], length 3
- curve.curvature(point)
-
Get the curvature of the Curve at a particular point.
curvature = curve.curvature([0,0,0])- Parameters:
-
point (tuple[float], length 3, in) – A vector containing 3 doubles representing coordinates of a location on the Curve
- Returns:
-
The curvature of the Curve at the location specified
- Return type:
-
tuple[float], length 3
- curve.closest_point(point)
-
Get the curvature of the Curve at a particular point.
close = curve.closest_point([0,0,0])- Parameters:
-
point (tuple[float], length 3, in) – A vector containing 3 doubles representing coordinates of a location on the Curve
- Returns:
-
The closest point to the Curve from the location specified
- curve.closest_point_trimmed(point)
-
Get the curvature of the Curve at a particular point.
close = curve.closest_point([0,0,0])- Parameters:
-
point (tuple[float], length 3, in) – A vector containing 3 doubles representing coordinates of a location on the Curve
- Returns:
-
The closest point to the Curve from the location specified
- Return type:
-
tuple[float]
- curve.length()
-
Get the length of the Curve.
len = curve.length()- Returns:
-
The length of the Curve
- Return type:
-
float
- curve.curve_center()
-
Get the center point of the Curve.
center = curve.curve_center()- Returns:
-
A vector containing the coordinates of the Curve’s center according to the following:
-
0 - x coordinate
-
1 - y coordinate
-
2 - z coordinate
- Return type:
-
tuple[float], length 3
- curve.position_from_fraction(fraction_along_curve)
-
Get the position of the point a specified fraction along the Curve.
pos = curve.position_from_fraction(0.5)- Parameters:
-
fraction_along_curve (float, in) – A decimal value between 0 and 1 to determine a particular position along the Curve
- Returns:
-
A vector containing the coordinates of the position a specified fraction along the Curve:
-
0 - x coordinate
-
1 - y coordinate
-
2 - z coordinate
- Return type:
-
tuple[float]
- curve.start_param()
-
Get the lowest value of the Curve in uv space.
start = curve.start_param()- Returns:
-
The beginning value of the parameter
- Return type:
-
float
- curve.end_param()
-
Get the highest value of the Curve in uv space.
end = curve.end_param()- Returns:
-
The ending value of the parameter
- Return type:
-
float
- curve.u_from_position(position)
-
Get the u value of a particular position on the Curve.
u = curve.u_from_position([0,0,0])- Parameters:
-
position (tuple[float], length 3, in) – A vector containing the coordinates of the input position
- Returns:
-
The u value of the position along the Curve
- Return type:
-
float
- curve.position_from_u(u_value)
-
Get the position of a particular u value for the Curve.
position = curve.position_from_u(0.5)- Parameters:
-
u_value (float, in) – The u value of the position along the Curve
- Returns:
-
A vector containing the coordinates of the output position
- Return type:
-
tuple[float]
- curve.u_from_arc_length(root_param, arc_length)
-
Get the u value for a point a specified arc length away from a specified root parameter on the Curve.
u = curve.u_from_arc_length(0, 0.5)- Parameters:
-
-
root_param (float, in) – The beginning parameter from which the arc length is added to
-
arc_length (float, in) – The length away from the root parameter of the output parameter
-
- Returns:
-
The u value of the Curve the arc length away from the root parameter
- Return type:
-
float
- curve.fraction_from_arc_length(root_vertex, length)
-
Get the fraction along the Curve a specified arc length is away from a given Vertex.
fraction = curve.fraction_from_arc_length(vertex, 0.5)- Parameters:
-
-
root_vertex (
Vertex, in) – The Vertex to start from (vertex object) -
length (float, in) – The length along the Curve away from the root Vertex
-
- Returns:
-
The fraction of the Curve that is the specified length away from the specified Vertex
- Return type:
-
float
- curve.point_from_arc_length(root_param, arc_length)
-
Get the position on a Curve that is a specified arc length away from the specified root parameter.
position = curve.point_from_arc_length(0, 0.5)- Parameters:
-
-
root_param (float, in) – The root parameter from which the arc length is added to
-
arc_length (float, in) – The arc length along the Curve away from the root parameter
-
- Returns:
-
A vector that contains the coordinates of a position a specified arc length away from the root parameter
- Return type:
-
tuple[float]
- curve.length_from_u(parameter1, parameter2)
-
Get the length between two specified parameters on a Curve.
length = curve.length_from_u(0, 0.5)- Parameters:
-
-
parameter1 (float, in) – The beginning parameter
-
parameter2 (float, in) – The ending parameter
-
- Returns:
-
The length between the two specified paramters along the Curve
- Return type:
-
float
- curve.is_periodic()
-
Get whether the Curve is periodic or not.
periodic = curve.is_periodic()- Returns:
-
Whether the Curve is periodic or not
- Return type:
-
boolean
- curve.dihedral_angle(other, common_surface)
-
Get the dihedral angle between this curve and another curve relate to the given surface.
Vertex
The Vertex class contains a Cubit vertex and provides methods to query the vertex.
- class cubit.Vertex(*args, **kwargs)
-
Defines a vertex object that mostly parallels Cubit’s RefVertex class
- vertex.color()
-
Get the color of the Vertex.
col = vertex.color()- Returns:
-
The color value associated with the vertex’s current color
- Return type:
-
tuple[float], length 4
- vertex.coordinates()
-
Get the Cartesian coordinates of the Vertex.
position = vertex.coordinates()- Returns:
-
A vector containing the coordinates of the Vertex with indices corresponding to the coordinates as follows:
-
0 - x coordinate
-
1 - y coordinate
-
2 - z coordinate
- Return type:
-
tuple[float]
Dir
The Dir class stores and manipulates a vector used as a direction.
- class cubit.Dir(x, y, z)
-
Defines a direction object
- vertex.x()
-
Get the x location of the point
- Returns:
-
x value
- Return type:
-
float See also: y(), z()
- vertex.y()
-
Get the y location of the point
- Returns:
-
y value
- Return type:
-
float See also: x(), z()
- vertex.z()
-
Get the z location of the point
- Returns:
-
z value
- Return type:
-
float See also: y(), x()
- vertex.set_x(x_in)
-
Set the x location of the point
- Parameters:
-
x_in (float) – the new x value
- vertex.set_y(y_in)
-
Set the y location of the point
- Parameters:
-
y_in (float) – the new y value
- vertex.set_z(z_in)
-
Set the z location of the point
- Parameters:
-
z_in (float) – the new z value
- vertex.get_xyz()
-
Get an array of the vector
- vertex.normalize()
-
Normalize ‘this’ vector :return: void :rtype: void
- vertex.set(x, y, z)
-
Set the xyz values of the vector
- Returns:
-
None
- Return type:
-
None
- vertex.cross(vec2)
-
Returns the cross product of this X vec2
- Returns:
-
cross product
- Return type:
- vertex.dot(vec2)
-
Returns the dot product
- Returns:
-
dot product
- Return type:
-
float
- vertex.length()
-
Returns the length
- Returns:
-
length
- Return type:
-
float
- vertex.distance(vec_in)
-
get the distance between two points
- Returns:
-
distance
- Return type:
-
float
- vertex.angle(vec_in)
-
Returns the interior angle of two vectors. The return the angle is in radians.
a = cubit.Dir(1,0,0) angle = a.angle(cubit.Dir(1,1,0))- Returns:
-
angle
- Return type:
-
float
- vertex.dir_print()
-
Print the output
- vertex.orthogonal_vectors()
-
Finds 2 (arbitrary) vectors that are orthogonal to this one